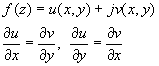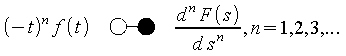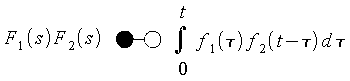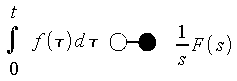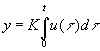- Absolute Konvergenz
- Allpaß
- Analytische Funktion
- siehe auch
holomorphe Funktion
- Anfangswertsatz
-
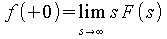
- Betragskennlinie
- BIBO-Stabilität
- Bildfunktion
- Charakteristische Gleichung
-
- CAUCHY-RIEMANNīsche
DG:
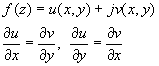
- Dämpfungsregel der Laplace-Transformation
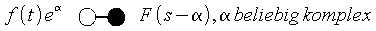
- Dämpfungen
- Dekade
Bedeutet hier die zehnfache Frequenz (f0, 10f0, 100f0,..). In der Akustik wird die doppelte Frequenz als Oktav bezeichnet.
- Differentiationsregel für die Bildfunktion
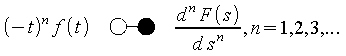
- DYNAMISCHE-KORREKTUR:
Zielt darauf ab, das dynamische Verhalten der Regelung zu verbessern, damit die Regelung die an sie gestellten Anforderungen erfüllen kann. Die dazu erforderlichen Maßnahmen werden als dynamische Korrektur bezeichnet. Oft spricht man auch von Stabilisierung , obgleich die Stabilisierung nur ein Teilziel ist, da die Regelung ja auf jeden Fall außerdem stationär genau und genügend schnell gemacht werden soll. Auch die Bezeichnung Synthese oder Entwurf der Regelung sind weithin üblich.
Im konkreten Fall besteht das Ergebnis der Korrekturmaßnahmen darin, daß ein zusätzliches Bauglied in die Regeleinrichtung eingeführt wird: die Korrektureinrichtung. In komplizierten Fällen kann sie auch aus mehreren, voneinander getrennten Baugliedern bestehen. In zunehmendem Maß wird sie nicht mehr in Hardware ausgeführt, sondern als Algorithmus in einem Prozeßrechner implementiert.
- Endwertsatz
-

- Faltungsregel der Laplace-Transformation:
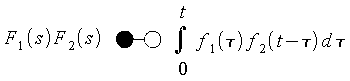
oder

- Frequenzgang
-
- Frequenzkennlinien
- (Frequenzcharakteristiken, Bode-Diagramm, Amplituden-Phasen-Diagramme)
- Führungsübertragungsfunktion
-
- Gewichtsfunktion
- g(t) Impulsantwort
- Gewöhnliche Differentiation
-
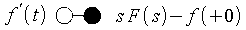
bzw. allgemein
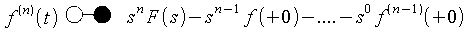

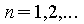
- Gütemaß
- IAE, ITAE, quadratische Regelfläche
- HOLOMORPHE (ANALYTISCHE,
REGULÄRE) FUNKTION
Eine Funktion f(z) heißt in einem Gebiet G analytisch,
regulär oder holomorph, wenn sie in allen Punkten von G
differenzierbar ist.
Die Funktion f(z) = u(x,y) + jv(x,y) ist genau dann in G
differenzierbar, wenn u und v stetige partielle
Ableitungen nach x und y in G besitzen und dort die
CAUCHY-RIEMANN schen
Differentialgleichungen gelten.
- Kriterien von Hurwitz und Routh
- Integrationsregel der Laplace-Transformation
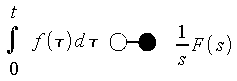
- I-Glied(Integrierglied)
- Funktionalbeziehung:
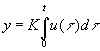
- Übertragungsfunktion:
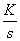
- Sprungantwort:
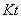
- Verlauf der Sprungantwort:
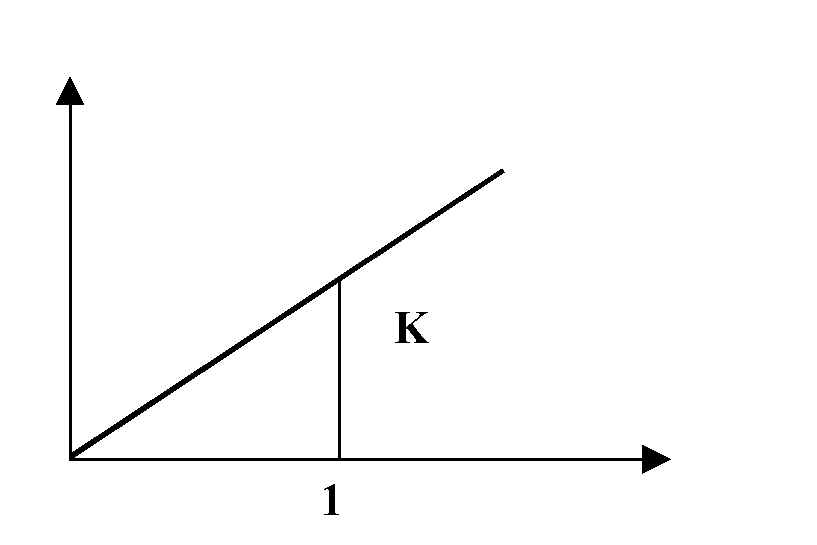
- Symbol
- (kein Eintrag)
- Knickpunktkorrektur:
- (kein Eintrag)
- Korrespondenz
- (kein Eintrag)
- Kreisverstärkung
- Kritische Stellen sλ
- LAPLACE-Integral
- LAPLACE-Transformation
- Linearitätsregel
- Ein Übertragungsglied heißt linear,
wenn
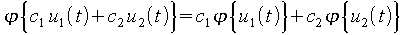
mit u1(t), u2(t),c1,c2 beliebig.
- Stabilitätskriterium nach LJAPUNOW
- Stabilitätsbegriff nach M.A. LJAPUNOW: Während bei den sonstigen im Kurs behandelten Stabilitätsdefinitionen die Anfangsbedingungen der zugrundeliegenden Differentialgleichungen zu Null angenommen werden und lediglich die Wirkung der Eingangsgröße untersucht wird, wird bei der Ljapunowschen Definition umgekehrt vorgegangen. Die Anregung wird zu Null angenommen und der Einfluß der Anfangswerte untersucht. Im einfachsten Fall geht man davon aus, daß das dynamische System in einem stationären Zustand (Gleichgewichtslage) gehalten werden soll, aber zum Anfangszeitpunkt, etwa durch vorausgegangene Störungen, aus dem stationären Zustand ausgelenkt wurde. Soll das System brauchbar sein, muß es von selbst in den stationären Zustand zurückkehren. Angewendet wird dieser Stabilitätsbegriff für die Stabilitätsuntersuchung an nichtlinearen Systemen.
- LZI-Glied (Lineares Zeitinvariantes
Glied)
- Ein Übertragungsglied, das der
Gleichung Y(s)=U(s)G(s),
bzw. y(t)=g(t)*u(t) genügt, ist linear
und zeitinvariant.
Diese Aussage gilt auch umgekehrt.
- (kein Eintrag)
- Minimalphasenglieder
- Nennerzeitkonstante
- Nyquistkriterium
-
- Offener Regelkreis
- Operator
-
-
Originalfunktion
- Ortskurve des offenen Regelkreises
- P-Regler
- G_k = K_R
- PD-Regler
- G_k = K_R
- PI-Regler
- G_k = K_R + modifizierte pi-regler
- idealer PID-Regler
- G_k = K_R ideal, real verallgemeinert
- PID-Algorithmus
- mit gemitteltem D-Anteil zusätzlich
- Partialbruchzerlegung:
-
- Phasenkennlinie:
-
- Phasenlineal:
-
Hilfsmittel zur Konstruktion der Phasenkennlinien beim Totzeit- und VZ1-Glied. Auf dem Phasenlineal sind zwei Skalen angebracht. Eine mit A bezeichnete Funktionsskala gibt die Abhängigkeit der zum Frequenzgang des VZ1-Gliedes gehörende Phase von w/w0 wieder. Man legt die Skala parallel zur w-Achse, und zwar so, daß der Mittelstrich gerade auf die Knickfrequenz w0 zeigt. Jeder Wert auf dieser Funktionsskala liegt über einem bestimmten Wert der w-Achse und gibt die zu diesem w-Wert gehörige Phase des VZ1-Gliedes an, sofern man ihn noch mit dem negativen Vorzeichen versieht. Ähnliches gilt für die Totzeitskala.
- Phasenrückdrehung:
-
Durch Einfügen von Zählerfaktoren in den Frequenzgang des offenen Kreises wird eine Phasenvordrehung, die die Gefahr der Instabilität erhöht, wieder kompensiert. Das positive Argument des Zählerfaktors bedeutet für den Fahrstrahl der Ortskurve des offenen Kreises eine Drehung im mathematisch positiven Sinn, also Phasenrückdrehung.
- Phasenvordrehung:
-
In der Regelungstechnik wird damit die Drehung des Fahrstrahles der Ortskurve im Uhrzeigersinn gemeint (mathematisch bedeutet dies eine negative Drehung in der komplexen Ebene) . Ein I-Glied verursacht so eine Drehung um -90°, so daß der Regelkreis Gefahr läuft, instabil zu werden. Es verursacht aber jede Nennerzeitkonstante eine Phasenvordrehung, und zwar um so mehr, je größer die Zeitkonstante T ist.
- (kein Eintrag)
- RATIONALE Funktion:

- R-GLIEDER
- Rationale Übertragungsglieder
- Regel für die Rechtsverschiebung der Originalfunktion bei der Laplace-Transformation:

- Reguläre Funktion:
- siehe auch
holomorphe Funktion
- Reihenstabilisierung:
- Einfügen von Faktoren in den Frequenzgang des offenen Kreises.Zähler der
- Stabilität
- Stabilitätskriterien
- algebraische, geometrische
- Grundlegendes Stabilitätskriterium
- Stationärer Regelfehler
- Stationäre Genauigkeit
- ε
- Stationärer Zustand:
- Auch als Ruhezustand,
Beharrungszustand und Gleichgewichtszustand bezeichnet.
Der stationäre Zustand ist dadurch gekennzeichnet, daß alle zeitveränderlichen Größen
konstante Werte einhalten.
Daher werden alle zeitlichen Ableitungen der Systemgrößen gleich Null.
Technische Systeme weisen im allgemeinen genau einen
stationären Zustand auf.
Es gibt jedoch auch Systeme, die mehrere stationäre
Zustände oder auch
gar keinen derartigen Zustand besitzen.
- Störübertragungsfunktion:
- Störwelligkeit:
-
Auch Rauschen genannt. Es handelt sich dabei um statistisch schwankende Zeitvorgänge, die den eigentlichen Zeitvorgängen der Anlage überlagert sind und in jedem realen System, mehr oder weniger stark, vorkommen.Verstärkt wird die Störwelligkeit durch D-Glieder (wenn die Differentation, wie i.a. üblich, nach der Zeit erfolgt). Diese Eigenschaft des D-Gliedes kann durch Einfügen von Nennerzeitkonstanten in Grenzen gehalten werden.
- Strukturbild:
- Totzeit
-
Totzeit des
- transzendente Gleichung
-
Totzeit des
- Übertragungsfunktion
- G(s)
- Übertragungsglied
- Verallgemeinerte Differentiation
-

bzw. allgemein
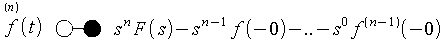

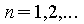
- VZ2-Lineal:
Hilfsmittel zur Konstruktion der Phasenkennlinien beim VZ2-Glied, bzw zur Knickpunktkorrektur. Es besteht aus durchsichtigem Material und trägt zwei Kurvenscharen, von denen eine zur Ermittlung des Betrages und die andere zur Bestimmung der Phase dient.
- Wurzelortskurve
- komplementäre WO erweiterte WO
- (kein Eintrag)
- (kein Eintrag)
- Zählerzeitkonstante
- Zeitinvarianz
- Ein Übertragungsglied heißt zeitinvariant,
wenn es auf die nach
rechts verschobene Eingangsgröße u(t-to) mit
der nach
rechts verschobenen Ausgangsgröße y(t-to) antwortet. , wenn also gilt:
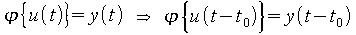
-
- (kein Eintrag)