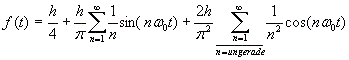| Fourierreihenapproximation |
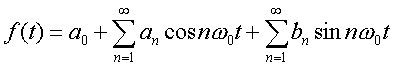
In der Praxis wird die Fourierreihe
nach einer endlichen Zahl n abgebrochen und es kommt
zu einer
Approximation durch ein trigonometrisches Polynom n-ten Grades.
Das Applet zeigt,
wie sich die Approximation durch Ändern des Grades
n an die Funktion annähert.
Zum Steuern des Applets wird
der Grad n mit den Button N+ oder N- stufenweise geändert.
In einer Animation, die mit Hilfe des Buttons Animation ein- und ausschaltet
werden kann,
wird der Grad n schrittweise bis 50 erhöht.
Direkt eingegebene Werte für n, zwischen 1 und 200,
werden
mit der Returntaste übergeben. Die Approximation wird an verschiedenen Funktionen,
die über das Funktionenfeld ausgewählt werden, vorgeführt.
Folgende Funktionen wurden für die Approximationen verwendet:
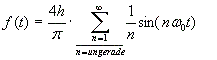
![]()
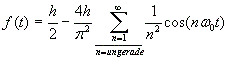
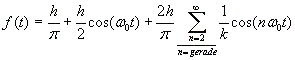
![]()