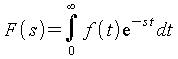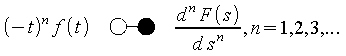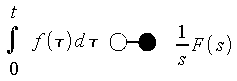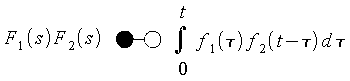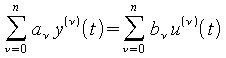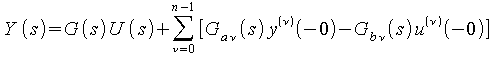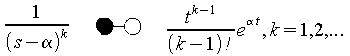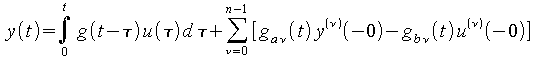Die durch das Laplace-Integral
(1.1)
vermittelte eindeutige Zuordnung einer Zeitfunktion f(t), der Originalfunktion, zu einer komplexen Funktion F(s), der Bildfunktion, heißt LAPLACE-Transformation.

Man schreibt


und bezeichnet das einander zugeordnete Funktionenpaar als eine Korrespondenz.

Für die in der Regelungstechnik vorkommenden Zeitfunktionen ist das Laplace-Integral in einer rechten Halbebene der s-Ebene absolut konvergent.Es stellt dort eine analytische Funktion dar, die in weitere Teile der s-Ebene analytisch fortgesetzt werden kann.

Linearitätsregel:
Die Laplace-Transformation ist eine lineare Transformation, d.h. es gilt



Differentiationsregel für die Bildfunktion:
Der n-maligen Differentiation der Bildfunktion F(s) nach s entspricht im Zeitbereich die Multiplikation von f(t) mit (-t)ⁿ:
(1.16)

Dämpfungsregel:
Die Multiplikation der Zeitfunktion f(t) mit dem Faktor e ^αt bedeutet im Bildbereich eine Argumentverscheibung von s nach s- α:
(1.18)

Integrationsregel:
Integriert man die Originalfunktion f(t) von 0 bis t, so ist die Bildfunktion durch s zu dividieren:
(1.53)

Regel für die Rechtsverschiebung der Originalfunktion:
Der Verschiebung der Zeitfunktion f(t) um t₀ nach rechts entspricht die Multiplikation der Bildfunktion F(s) mit dem Faktor e^-t₀s, sofern f(t) = 0 für t < 0 vorausgesetzt ist:

(1.56)
Eine allgemeine Formulierung bei f(t) ungleich 0 für t < 0 ist in Tabelle 1/1 zu finden.

Faltungsregel der Laplace-Transformation:
Dem Produkt zweier komplexer Funktionen entspricht die Faltung der zugehörigen Zeitfunktionen, d.h. :

(1.48)
oder abgekürzt
(1.50)
Die durch das Faltungsintegral in Glg. (1.48) bewirkte Verknüpfung der beiden Funktionen f₁(t) und f₂(t) wird als Faltung oder Faltungsmultiplikation bezeichnet, da sie wie die Zahlenmultiplikation kommutativ, assoziativ und distributiv ist.

Aus der analytischen Operation des Differenzierens wird im Bildbereich die elementare Operation des Multiplizierens mit der Variablen s.

Gewöhnliche Differentiation
Bei der gewöhnlichen Differentiation kann man an den Sprungstellen nicht differenzieren; es gilt:

(1.22)
bzw. allgemein


(1.24)

Verallgemeinerte Differentiation
Bei der verallgemeinerten Differentiation, wie sie ein technisches System ausführt, werden an Sprungstellen δ-Funktionen erzeugt; es gilt:

(1.31 )
bzw. allgemein


(1.32)

Die Lösung von Differentialgleichungen des Typs

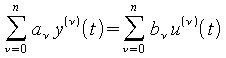
(1.57)


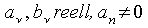
mit Hilfe der Laplace-Transformation erfolgt in vier Schritten:

Schritt 1: Laplace-Transformation der gegebenen Differentialgleichung
Als Resultat erhält man eine lineare algebraische Gleichung für die Laplace-Transformierte Y(s) der gesuchten Zeitfunktion y(t).

Schritt 2: Auflösung der algebraischen Gleichung nach Y(s)
Als Lösung ergibt sich eine Beziehung der Form:


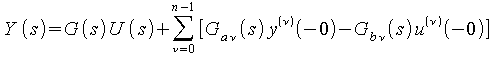
(1.58)

Darin sind rationale Funktionen, deren Zählergrad höchstens gleich dem Nennergrad ist.

Insbesondere ist
(1.59)


Schritt 3:Partialbruchzerlegung der rationalen Funktionen

Dabei muß nur die eine charakteristische Gleichung
(1.60)
gelöst werden.

Schritt 4:Rücktransformation
Man übersetzt die Partialbrüche mittels der Korrespondenz
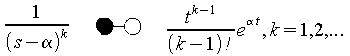
(1.20)
in den Zeitbereich und erhält so die Zeitfunktion

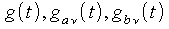
Die allgemeine Lösung der Diffentialgleichung (1.57) lautet dann:


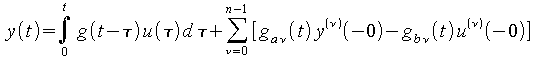
(1.61)

Das Faltungsintegral gibt den Einfluß der Eingangsgröße oder Anregung u(t) wieder, während der Summenterm zeigt, wie sich die Vergangenheit des Systems auf den Zeitraum t > 0 auswirkt.
Ist die Laplace-Transformierte U(s) der Anregung u(t) eine rationale Funktion, so ist das gesamte Produkt G(s) U(s) rational und kann in Partialbrüche zerlegt werden.
Diese werden gemäß (1.20) rücktransformiert.
Damit ist die Lösung y(t) gefunden, ohne das Faltungsintegral in (1.61) explizit berechnen zu müssen.

Die Lösung eines Systems von linearen Differentialgleichungen mit konstanten Koeffizienten mittels der Laplace-Transformation erfolgt entsprechend wie bei einer Differentialgleichung in vier Schritten:

Schritt 1: Laplace-Transformation der Differentialgleichung
Man erhält so ein System von linearen algebraischen Gleichungen für die Laplace-Transformierten der gesuchten Zeitfunktionen.

Schritt 2: Auflösung des algebraischen Gleichungssystems nach den gesuchten Funktionen
Als Lösung ergeben sich Gleichungen vom Typ (1.58)

Schritt 3: Partialbruchzerlegung.

Schritt 4: Rücktransformation
Rückübersetzung der einzelnen Partialbrüche mit Hilfe der Korrespondenz (1.20) und evtl. Anwendung der Faltungsregel.

Die Grenzwertsätze ermöglichen es, das Grenzverhalten der Originalfunktion direkt aus der Bildfunktion zu bestimmen, ohne daß man die Originalfunktion selbst berechnen muß.

Anfangswertsatz:


, sofern der Grenzwert der Zeitfunktion existiert und endlich ist.


Endwertsatz:


, sofern der Grenzwert der Zeitfunktion existiert und endlich ist.